One of the earliest and most interesting data science projects we’ve embarked on is automatically learning which professional skills relate to one another, based on our data. For instance, if someone lists data science as a skill, it’s likely they also know machine learning, R or python and Hadoop. This project has a lot of potential uses on our site, from suggesting related skills when a user adds technology skills to their profile, to enhancing our search and job recommendation platforms by matching across related skills. This can also be used to suggest related keywords when a user is typing in a search query:
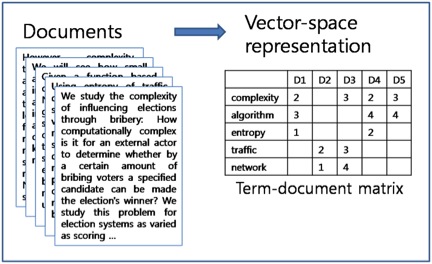
How do we determine if two different words are related? A research area in the field of Natural Language Processing, called “Distributional Semantics,” addresses this problem. Distributional Semantics attempts to determine the meaning of a word by examining the different contexts in which it occurs. To quote John Firth, a pioneer in this field, “a word is characterized by the company it keeps”; by looking at the words that occur within the same context as the original word, such as the same sentence or document, you can understand the word’s meaning. That means if you look at a lot of documents about cars, you’ll see terms such as “tires”, “wheels”, and “automobiles” occurring in a lot of the same documents. You can then use these co-occurrence statistics to determine which terms relate to one another. Check out the latest data science jobs. So how did we turn this concept into an algorithm that can learn related technology skills? First we used a parser we developed to extract technology skills from job postings. Then we constructed a “Term-Document Matrix” from these lists of skills. Also called a “Vector Space Representation,” this matrix features a row per skill, along with a column for each document (or job in this case), as illustrated below:
(from http://mlg.postech.ac.kr/research/nmf)
Incidentally, this is the data structure used by search engines for performing Web searches. In this format, each skill is represented as a vector (a list of numbers) encoding the documents in which it occurs (hence the term ‘Vector Space Representation’). However, a skill is clearly more important to some documents than others; for instance, Java is a more important skill to a Java developer than to a Scala or Hadoop developer. To reflect this, we use a weighting scheme called tf-idf weighting also borrowed from the field of Information Retrieval, which studies search engine design. The tf-idf calculation multiplies a measure of term frequency (tf)—how often a word occurs in the current document—with inverse document frequency (idf), which measures how rarely the word appears in a set of documents. The intuition behind tf-idf is that words that are important to a document occur in that document much more frequently than they do in most other documents. A lot of prior research has shown that weighting words in this way is very effective for determining which words best represent a document. Now that we have tf-idf vectors, we can compute similarities between pairs of skills by computing the similarity of their vectors. However, using the raw tf-idf vectors poses some problems. There is a lot of inherent noise in the data, as is typical with textual data, and we’d like much smaller vectors to work with. We typically take a sample of 100,000 jobs to compute skill similarities, which means each vector has 100,000 elements. We can solve these two problems by performing a dimensionality reduction on the data, reducing the number of elements per vector from 100,000 to 1,000, using an algorithm called truncated singular value decomposition. Dimensionality reduction can be considered a form of lossy data compression, wherein we compress the data by removing noisy data points that capture the least variation in the data, and combining columns that are very similar to form the new columns. This is important for matching rare skills. To create the term-document matrix and perform the dimensionality reduction, we use the python gensim package and the gensim LSA module, but we do the dimensionality reduction over the document and not the term dimension, which is how LSA normally works. LSA is computationally intensive, but gensim uses an iterative approximation, which is very fast and scales very well. Once we have these 1,000 dimensional vectors for each skill, we can use the cosine similarity metric to calculate how similar two skills are from their vectors, and thus compute the most similar skills for a given skill. Here are some examples of skills with their five most similar related skills: Data Science: Machine learning, Apache Flume, HDFS, Big data, Product marketing Linux: Unix, Linux administration, Red Hat Linux, C++, Apache HTTP Server Java: J2EE, Spring, Hibernate, Web services, Apache Struts HTML: CSS, JavaScript, jQuery, Web development, UI Networking: Cisco, Network engineering, Network management, Hardware, Cisco Certifications Project Management: PMP, Project planning, IT project management, Budget, Microsoft Project I think that’s pretty cool, given we’re generating that automatically from job descriptions posted on our site. We also tried using the resume dataset, but the results were of a lower quality, as the skills extracted from resumes can be from different jobs. Another interesting thing: we now have a way to compute the similarity of skills, by clustering groups of similar skills into groups of related items. We can use an off-the-shelf clustering algorithm to cluster the skill vectors by their cosine similarity; for this, I used affinity propagation, a popular graph-clustering algorithm because it’s known to work well on short documents. Unlike other clustering algorithms such as k-means, where you have to specify the cluster size, affinity propagation automatically discovers the number of clusters in a dataset. Here’s some example clusters, with some descriptive labels: Microsoft BI Stack: MDX, Microsoft BI, Microsoft SSAS, Microsoft SSIS, Microsoft SSRS Design Skills: Adobe CS, Adobe InDesign, Animation, Brand, Graphics, Interface design, Logos, Typography Java Frameworks: Apache Struts, GWT, Hibernate, J2EE, Java, Spring, Spring MVC Big Data NoSql: Apache Cassandra, Big data, MongoDB, NoSQL, Scalability Web Technologies: Ajax, CSS, HTML, HTML5, JavaScript, Responsive design, UI, Web development, jQuery, jQuery UI Data Science AI: Artificial intelligence, Data mining, Data science, Machine learning, Natural language processing Simon Hughes is the chief data scientist of the Dice Data Science Team.
Bibliography
Firth, J. R. (1957). A synopsis of linguistic theory 1930-1955. Oxford Philological Society.
Upload Your ResumeEmployers want candidates like you. Upload your resume. Show them you're awesome.